Module: Editor
Version: 4.2.1 +
User: Developer
Difficulty: Easy
Introduction
In this exercise a formula must be created that uses the Pythagorean Theorem to calculate the side-length of a triangle.
Prerequisites
- The Futurama Editor must be installed.
- Completing the tutorial Creating formulas with Futurama first, is recommended.
Description
The image at the right shows a triangle with the sides named A, B and C. 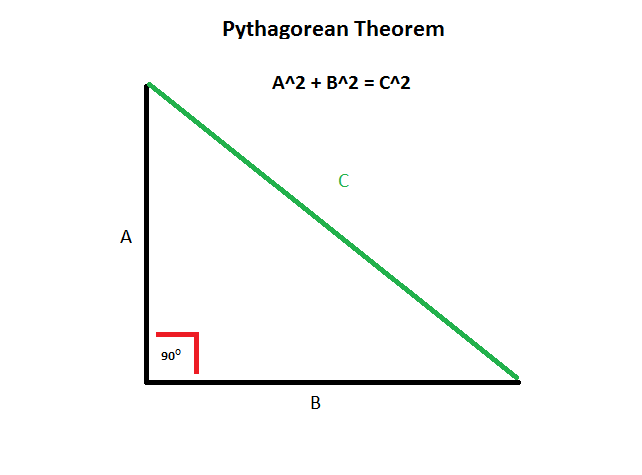
Side A has a fixed size of 3 inches. The length of side B is variable. The triangle is right-angled, so the angle between A and B measures 90°.
This means that the Pythagorean theorem applies:
A^2 + B^2 = C^2
Assignment
Create a formula that calculates C, where A has a fixed value of 3, and B is an input-argument.
Determine C for the following values of B:
- (A=3) B=3 C=
- (A=3) B=4 C=
- (A=3) B=5 C=
Tips
- You should create a formula of type 'double', as the length of size C does not need to be an integer.
- Futurama supports all basic arithmetic formulas. However, there's no special root function in Futurama, as you can formulate a (square) root in a general way by using the power-function.
Solutions
Answers
- (A=3) B=3 C=4.24 (rounded)
- (A=3) B=4 C=5
- (A=3) B=5 C=5.83 (rounded)
Download

You can download our solution for this assignment by clicking the image at the right. (Futurama 4.2.1.2)
Please note that you can very well have a different solution that is just as good as ours.
Printscreens
The printscreens of our solution can provide you some insight in how you should implement this exercise:
Variations
If you want some more practise on this subject, you could try the extra exercises below.
We won't provide a solution for these variations, just consider them as a way to further experiment with Futurama.
- (Easy:) Extend your formula by rounding the results to two digits.
- (Medium:) Extend your formula by adding size A as an argument.
- (Difficult:) Create a formula that determines if the value of C is an integer, based on the value for B. The formula should be a Boolean formula like: c(b)= Round(c(b)).